
Effective annual rates are essential foundations for treasury decision making because we often need to evaluate alternative investments or borrowings. To make the best decision, we need to make alternatives properly comparable. Headline interest rates are important, but they don't tell the whole story.
HOW MUCH AND HOW OFTEN
Two key numbers treasurers always need are:
- The nominal annual rate of interest (R); and
- How often the interest is compounded per year (n).
The frequency of the interest can have a significant impact on the value of the deal. Let’s see how this works, with a practical example.
ONCE PER YEAR
Say we’re in the happy position of having £100m to deposit, for 12 months. The first deal we look at pays 6% per annum, compounded once per year. This means the interest is calculated and added to the balance once only, at the end of the 12-month period.
INTEREST AND EFFECTIVE ANNUAL RATE (EAR)
We invest our £100m. The amount of interest is:
100 x 0.06 = £6m
The whole £6m is paid at the end of the 12-month period.
The EAR is the total accumulated interest, divided by the initial investment. In this case:
£6m / £100m = 6%
A BETTER DEAL?
Now we find a similar 6% deal, with one important difference. The compounding frequency will be greater. Interest will be calculated and added twice per year (n = 2). The nominal annual rate (R) is still 6%, the same as for the first deal.
PERIODIC INTEREST RATE
The periodic interest rate (r) per six months
is now:
r = R / n
= 6% / 2 = 0.03 per six months
HALF AS MUCH, TWICE AS OFTEN
Previously, we were getting 6% at the end of 12 months. Now, we’ll receive 3% every six months.
It’s always beneficial to receive money earlier. In this case, we get half our interest six months early.
Can we quantify this timing benefit? Happily, we can.
HOW MUCH BETTER?
The EAR puts a number on the benefit of the timing (n), combined with any differences in nominal annual rates (R).
We will often be weighing up a better EAR against greater risks or other costs.
Treasurers use EAR evaluations both for investments and for borrowings.
We’ll continue to focus on investments, but the principles are exactly the same for borrowings.
EAR DEFINITIONEAR usefully benchmarks the rates on different investments, on a standardised comparable basis. |
EAR ASSUMPTIONS
The definition of EAR makes two important assumptions:
(1) Intermediate interest is reinvested; and
(2) The rate on the reinvested interest is the same as the rate on the original deal.
EXAMPLE 1.
Compound interest
Based on compound interest, your organisation deposits £100m at a periodic interest rate of 3% per six months, for a total of 12 months.
Calculate:
(a) The balances at the end of each six-month period;
(b) The total interest earned in the12 months; and
(c) The effective annual rate.
ANSWER 1.
(a) Balances: interest on interest
The key to understanding this question is to recognise there is interest on interest.
We assume the periodic interest is rolled up within the investment.
Interest rolling up
| £m | Pd1 | Pd2 |
| Opening | 100 | 103.00 |
| + Interest at 3% | 3 | 3.09 |
| = Closing | 103 | 106.09 |
(b) Total interest
The total accumulated interest for the year is:
106.09 – 100 = £6.09m
(c) Effective annual rate
To make deals comparable, it’s useful to express this accumulated total interest as an annual percentage.
6.09 / 100 = 6.09%
WHY IS IT MORE THAN 6%
The EAR of 6.09% exceeds the nominal annual rate (R) of 6%, by 0.09%. This is because of the interest on interest assumed
in the EAR definition:
3% x 3% = 0.09%
EAR FORMULA
We can also work out the EAR with a formula:
EAR = (1 + r)n – 1
Where:
r = periodic interest rate
n = number of compounding periods per year
APPLYING THE FORMULA
r = 0.03 per six months; n = 2
EAR = 1.032 – 1
= 6.09%, the same answer as we got before.
The greater the EAR, the better the rate of income we enjoy.
EXAMPLE 2.
Let’s try increasing the compounding frequency again, and see if we get a further improvement.
Quarterly interest
Your organisation deposits £100m at a nominal annual interest rate of 6%.
Interest is calculated and added to the rolled-up balance every quarter.
Calculate:
(a) The effective annual rate; and
(b) The total interest earned for the 12 months.
(a) EAR = (1 + r)n – 1
R = 0.06; n = 4
r = 0.06 / 4 = 0.015
EAR = 1.0154 – 1
= 6.14% (to the nearest 0.01%)
(b) Total interest for year
This is the initial investment multiplied by the EAR:
100 x 0.0614 = £6.14m
That’s even better than the £6.09m we enjoyed with six-monthly compounding.
EVEN MORE OFTEN
If we continue our calculations, increasing the compounding frequency even more, we see a clear pattern. The more often the interest is compounded, the greater the EAR becomes.
Greater (n) = Greater EAR
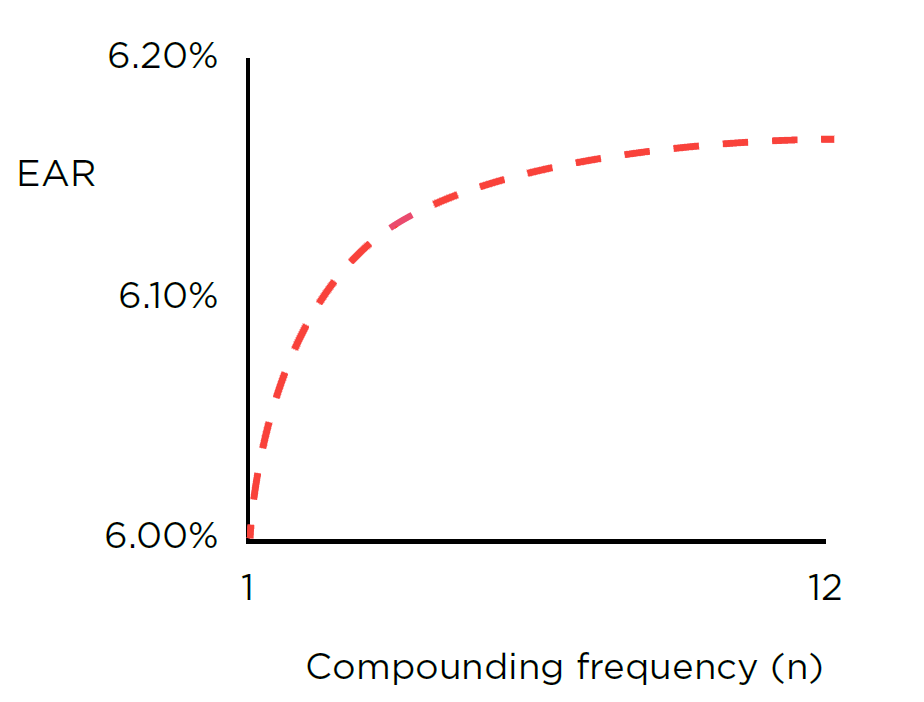
If the alternatives being compared were identical in all other ways, we would normally choose the one with the best EAR.
BEST CHOICES
However, the best EAR won’t necessarily be the best deal overall. We need to consider other factors, beyond EAR.
These important factors include risk, liquidity, flexibility, maturity and treasury policy. For example, higher risk investments are often prohibited.
The greater any financial stresses or other constraints, the more risk averse our approach will be. To make the best choices, we must master EAR, and then go beyond it.
____________________
Author: Doug Williamson
Source: The Treasurer magazine
