
Simple interest makes interest calculations easier, but it adds complexity to yield curve conversions. Take a look at a reliable method to making it easier.
JARGON BUSTING
First of all, let’s clarify:
|
1. YIELD CURVE
A yield curve describes today’s market rates per annum for fixed-rate funds with different maturities.
For example:
Table 1: Zero coupon rates
| MATURITY (months) | QUOTED RATE PER ANNUM |
| 0-3 | 4.0% |
| 0-6 | 4.2% |
| 0-9 | 4.4% |
Today’s quoted interest rate for 0-3 month funds is 4% per annum. The quoted rates for longer maturities are slightly higher.
2. SIMPLE INTEREST
The simple interest basis is a longstanding market convention. It was designed to make interest calculations quick and reliable, before the invention of modern calculators.
Simple interest calculates actual interest and quotes rates, with no interest on interest incorporated into the quoted market rate per annum. The simple interest basis is the market convention for quoting interest rates for short-term periods. ‘Short term’ means up to, and including, one year.
Actual interest for a given period is then worked out from the simple interest quote by a straightforward multiplication of the quoted annual rate. To illustrate, let’s work in sterling and use whole months. To keep
our numbers as easy as possible, let’s deposit exactly £1, for 0-3 months.
There are, of course, 12 months in a year (not three). So the actual interest payable for the three-month period (3/12 of a year) is not the quoted 4%, but rather:
(3/12 x 0.04) x £1 = £0.01.
This actual interest amount is also known as the ‘periodic interest’.
The total cash (principal + interest) we get back after three months is:
£1.01 (= (1 + (3/12 x 0.04)) x £1).
Similarly, the total interest for a 0-6 month deposit (6/12 of a year) at a quoted rate of 4.2% per annum (from Table 1, above) is:
(6/12 x 0.042) x £1 = £0.021.
And the total cash we get back after six months is:
(1 + (6/12 x 0.042)) x £1 = £1.021
Your turn now.
Please calculate (i) the interest and (ii) the total cash returned, from a 0-9 month deposit of £1. The quoted rate per annum is 4.4%. The answers appear at the end of this article1
3. ZERO COUPON RATE
All of the rates we’ve worked with so far have been zero coupon rates. They all apply to cash deposited or borrowed today (Time 0) and returned with all of the interest at the very end.
For example, our 0-6 month deposit above involves the following cash flows:
(1) We pay £1 now and
(2) We get back (1 + (6/12 x 0.042)) x £1 = £1.021 after six months.
4. FORWARD RATE
Forward interest rates are slightly different. These are rates that we can lock into today, for fixed deposits or borrowings starting in the future.
Table 2: Forward rates
| MATURITY (months) | QUOTED RATE PER ANNUM |
| 0-3 | 4.0000% |
| 3-6 | 4.3564% |
For example, the rate for 3-6 months funds is 4.3564% per annum. This means we can lock ourselves in today, to deposit cash three months from now, to get back our cash with pre-agreed interest after a further three months. Interest will be calculated at the pre-agreed interest rate of 4.3564% per annum, applied for 3/12 of a year.
This 3/12 factor is needed because the forward period of 3-6 months is three months long.
Assume cash available to deposit of £1.01.
This also happens to be the amount available from our earlier maturing deposit for 0-3 months (= (1 + (3/12 x 0.04)) x £1). Locking ourselves in today, to deposit this £1.01 at:
- Time 3 months will return:
(1 + (3/12 x 0.043564)) x £1.01 = £1.021 at Time 6 months.
This is exactly the same amount of cash as we received from our alternative zero coupon deposit for the entire period 0-6 months, which also gave us back £1.021
(see ‘Simple interest’ section earlier).
NO FREE LUNCHES
Our two calculations above are examples of the ‘no free lunch’ principle. Both alternative ways of structuring a 0-6 month deposit produce exactly the same six-month cash flow of £1.021.
If the two equivalent deals didn’t produce exactly the same final cash flow of £1.021, everyone in the market would prefer the better deal. Supply and demand in the market would then cause market prices to change, until the related cash flows came back into an exact balance, as before.2
This is known as the ‘no arbitrage’ market pricing principle. We can use ‘no arbitrage’ to calculate implied forward interest rates, converting from given zero coupon rates.
CALCULATING FORWARD QUOTES: 3-6 MONTHS
The forward market rate of interest (or return) links two related future cash flows in the market.
For example, the final cash flows from our two zero coupon deposits:
- £1.01 at Time 3 months
- £1.021 at Time 6 months
We can make a commitment today to deposit £1.01 in three months’ time, for a further three-month period. That deposit must return £1.021 at its maturity of Time 6 months. This is the ‘no arbitrage’ principle, illustrated:
The related periodic rate of return is given by: ((Cash at end) ÷ (Cash at start)) – 1
In this case, periodic rate:
(£1.021 ÷ £1.01) – 1
= 1.0891% interest per three months.
As we’ve seen, short-term interest rates are quoted as simple rates per annum.
Therefore, the (simple annual) quoted rates are multiplied by 3/12 to work out the actual interest for a three-month-long period. So to convert the periodic rate for three months (1.0891%) to a simple quoted annual rate, we need to make the opposite adjustment.
That is, multiply by 12/3:
1.0891% x 12/3
= 4.3564% quoted forward rate per annum, for 3-6 months maturity.
4.3564% is indeed the figure that we saw before in Table 2 and that we have already validated in the section titled ‘Forward rate’ earlier. So our ‘no arbitrage’ conversion, to convert zero coupon rates to forward rates, produces the right answer.
CALCULATING FORWARD QUOTES: 6-9 MONTHS
It’s your turn again.
You calculated before that the final cash flow from a 0-9 month deposit of £1 quoted at 4.4% per annum is £1.033. Make sure that you’re still happy with this calculation. If you need to refresh yourself, see answer 1 at the end of this article.
Now use (1) the £1.033 at nine months and (2) the £1.021 at six months (from our 0-6 month zero coupon deposit) to work out the 6-9 month forward quote.
Clue: follow the pattern above of: ((£1.021 ÷ £1.01) – 1) x 12/3, but roll everything forward by three months. Answer at the end.3
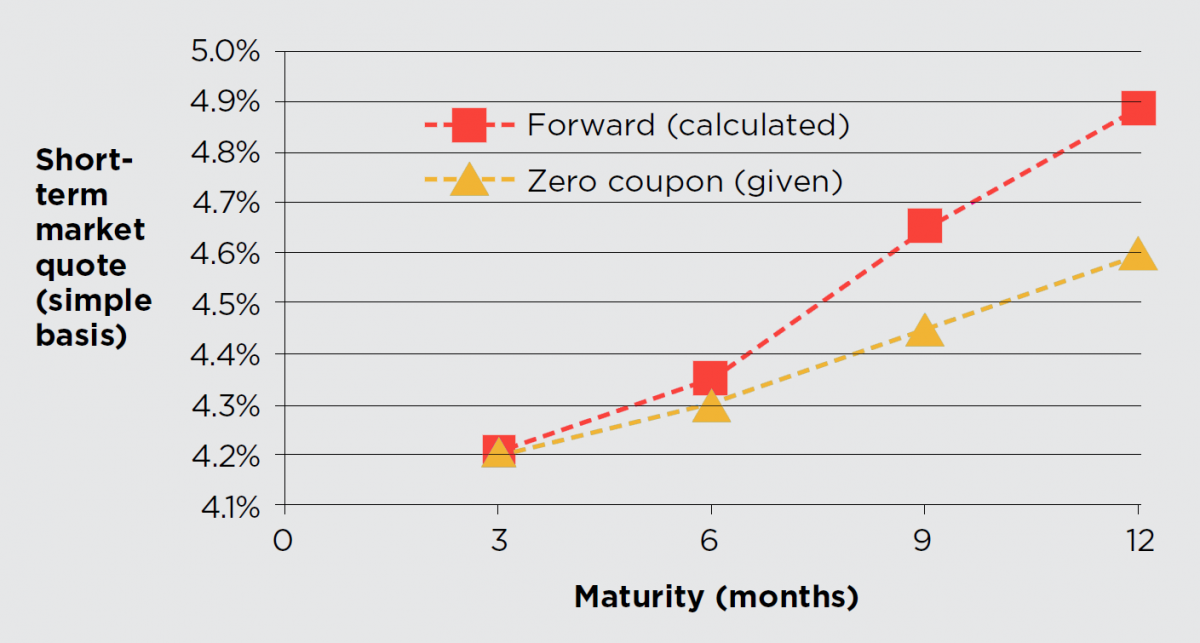
Use the GBP market zero coupon rates (▲) quoted below to calculate the related forward rate quotes for the periods
3-6 months, 6-9 months4 and 9-12 months5.
3 months: 4.205%
6 months: 4.300%
9 months: 4.450%
12 months: 4.600%
The first answer (■)
3-6 months quote:
((1 + (6/12 x 0.043) = 1.0215) ÷ (1 + (3/12 x 0.04205) = 1.0105125)) – 1
= 1.08732%
x 12/3
= 4.3493% 3-6 months quote per annum.
Finish the question off now, for 6-9 months4 and 9-12 months5. If you’re not sure, follow the pattern of the similarly structured examples above.
____________________
Author: Doug Williamson
Source: The Treasurer magazine
Want to learn more about treasury and cash management?
Choose from:
• eLearning courses: 45-90 minutes to complete, available online 24/7.
• Training courses: live skills-based training sessions.
• Treasury and Cash Management qualifications: internationally recognised courses from entry to master level.
All our courses will provide you with valuable knowledge as well as easy-to-share digital credentials to demonstrate your learning achievements.
Discover more resource articles
|
ANSWERS 1 Interest £0.033 = (9/12 x 0.044) x £1. Total cash £1.033 (= (1 + (9/12 x 0.044)) x £1). 2 In practice, these price adjustments are almost instantaneous, because of computer-driven trading. 3 Periodic rate (3 months) = (1.033 ÷ 1.021) – 1 = 1.17532%. Quote per annum x 12/3 = 4.7013%. 4 ((1 + (9/12 x 0.0445) = 1.033375) ÷ 1.0215) – 1 = 1.16251%: x 12/3 = 4.6500%. 5 ((1 + (12/12 x 0.046) = 1.046) ÷ 1.033375) – 1 = 1.22172%: x 12/3 = 4.8869%. |
