
Capital structuring and managing our organisation’s cost of capital are essential treasury skills. Take a look at a powerful weighted averaging technique to improve the speed and transparency of this work.
COST OF CAPITAL
All companies are funded by equity capital and must also have debt. Each of these sources of capital has a cost , conventionally expressed as an annual percentage of its current market value.
OPERATING RETURNS
The returns out of which our cost of capital has to be met or exceeded are the cash surpluses from our operations. Any projects or operations that don’t achieve the cost of capital will destroy value.
So it is an essential practical skill to be able to calculate and explain cost of capital quickly and confidently, in order to evaluate new proposals and continuing operations.
Let’s look at some examples...
COST OF EQUITY
£3m of equity, costing a company 8% per annum, needs:
£3m x 8% = £0.24m per annum
This is the amount required by the equity investors.
The equity investors’ expected annual shareholder return is the same percentage of 8%, on their investment of £3m:
£0.24m ÷ £3m = 8%
COST OF DEBT
£1m of debt, costing the company 4% per annum after tax relief, needs:
£1m x 4% = £0.04m per annum
The cost of debt is cheaper for the company, but debt is also a more risky source of capital for the borrower. Equity is less risky
for the company, but more expensive.
WEIGHTED AVERAGE COST OF CAPITAL
The average percentage cost of all sources of capital in combination is calculated as the company’s weighted average cost of capital (WACC). For a listed company, WACC changes continuously, as market values fluctuate.
A simplistic averaging technique would be to add up each of the items, and divide by the total number of items. However, this is normally too limited to give an accurate enough answer for financial evaluations.
Instead, we need a weighted averaging calculation. The best weightings to use are normally current market values. This technique of weighting by market values has many useful applications in finance, not only WACC calculations.
ALL EQUITY (100%)
Let’s start with a case where the proportion of equity funding is 100%, and the cost of equity is 8%, as before. The weighted average cost of capital is simply 8%, the same as the cost of equity.
This would normally be the most conservative, safe and flexible capital structure. The safety and flexibility enjoyed are being paid for by a relatively high WACC.
EQUAL WEIGHTINGS (50%)
Another simple case is where the proportions of debt (D) and equity (E) are exactly equal. In this case the WACC will be exactly halfway between the lower cost of debt and the higher cost of equity. This relationship is illustrated in the see-saw diagram:
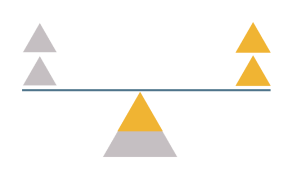
We can also set out the calculation in a table.
| WEIGHTING | X COST | = WEIGHTED COST | |
| D | 2 | 4% | 8% |
| + E | 2 | 8% | 16% |
| =(D + E) | 4 | 24% |
WACC = Total weighted cost ÷ (D + E)
= 24% ÷ 4
= 6%
This is the weighted average when the weightings are equal. It is exactly halfway between 4% and 8%. This company is enjoying a lower WACC, but it is a more risky and less flexible capital structure than all-equity.
WEIGHTED TOWARDS EQUITY (75%)
A more conservative compromise response would be to use a greater proportion of equity funding, perhaps 75%. Now the balancing point of our see-saw moves to the right. The weighted average moves closer to the equity cost of 8%.
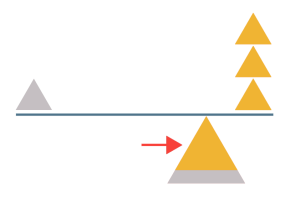
| WEIGHTING | X COST | = WEIGHTED COST | |
| D | 1 | 4% | 4% |
| + E | 3 | 8% | 24% |
| =(D + E) | 4 | 28% |
WACC = Total weighted cost ÷ (D + E)
= 28% ÷ 4
= 7%
Changing the balance of equity to debt, in the direction of more equity, has increased the weighted average cost of capital.
The WACC of 7% still lies in between the debt cost of 4% andthe equity cost of 8%.
TRY AN EXAMPLE YOURSELF
This example is based on a question in the Certificate in Treasury Fundamentals Specimen paper - you can find the answer at the bottom of the page.
APP Group is funded by £5m of debt and £20m of equity.
Its annual cost of debt is 5% and the expected annual shareholder return is 7%.
What is APP Group’s weighted average cost of capital?
A 5.6%
B 6.0%
C 6.6%
D 7.0%
____________________
Author: Doug Williamson
Source: The Treasurer magazine
|
The answer is C: 6.6%. This is in between 5% and 7%, but closer to the equity cost of 7%, because APP has more equity than debt.
|
Want to learn more about treasury and cash management?
Choose from:
• eLearning courses: 45-90 minutes to complete, available online 24/7.
• Training courses: live skills-based training sessions.
• Treasury and Cash Management qualifications: internationally recognised courses from entry to master level.
All our courses will provide you with valuable knowledge as well as easy-to-share digital credentials to demonstrate your learning achievements.
